Производная функции

Производная функции — это предел отношения приращения к аргументу при условии, что приращение аргумента стремится к нулю:

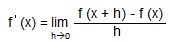Дифференцирование — операция нахождения производной.

Правила дифференцирования

1. Производная суммы равна сумме производных:
   (f(x) + g(x))' = f' (x) + g' (x).
2. (c·f(x))' = c·f' (x), где с — постоянный множитель.
3. Производная произведения:
   (f(x) · g(x))' = f' (x) · g(x) + f(x) · g' (x).
4. Производная частного:
   
5. Производная сложной функции:
   (f(g(h(x))))' = f' (g(h(x))) · g' (h(x)) · h' (x).

Геометрический смысл производной

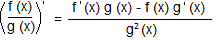
Геометрический смысл производной: f' (x) есть угловой коэффициент касательной к графику функции y = f (x) в точке (x; f (x)).
Уравнение касательной к графику функции y = f (x) в точке (x_о; f( x_о)):
y = f (x_о) + f' (x_о) (x - x_о)

Другие заметки по алгебре и геометрии