26.03.2012
Авторы: Козлов В. Н., д.т.н., профессор, заведующий кафедрой «Системный анализ и управление» и Кимков В. Н., к.п.н., доцент кафедры «Системный анализ и управление» Санкт-Петербургского государственного политехнического университета.
В основу создания академических педагогических измерительных материалов (АПИМ) можно положить интеллектуальные технологии и теорию знаний. Компетентностное содержание можно структурировать на основе методов теории знаний и интеллектуальных технологий.
Как сформулировал американский экономист и публицист Д. Гелбрейт: «Технология — это систематизированное применение научного (организованного) знания для решения практических задач».
«Технология по С. С. Гусеву» — это некоторый способ человеческого отношения к окружающей действительности, порожденный практической ориентированностью познания.
«Технология по В. П. Каширину» определяется как прогрессирующая и управляемая человеком природно-социальная совокупность процессов целенаправленного изменения различных форм вещества, энергии и информации, протекающая в различных системах в соответствии с их специфическими законами строения и функционирования.
«Технология по А. И. Ракитову» включает: инструментальную систему; совокупность операционных процедур; систему деятельности, детерминированную инструментальной системой и влияющую на нее; систему управления соответствующей деятельностью; совокупность последствий (социальных и экономических); информационную среду, в которой эта деятельность осуществляется.
Интеллект — способность к мышлению и рациональному познанию. Определим интеллектуальный потенциал личности как уровень его интеллекта. В процессе обучения на первых этапах в основном формируется информационный потенциал как набор сведений в рамках совокупности учебных дисциплин или информации.
Очевидно, что эти два понятия связаны друг с другом, поскольку информационный потенциал естественным образом формирует интеллектуальный потенциал и наоборот. На этой основе можно констатировать в образовании и науке «интеллектуально-информационный дуализм».
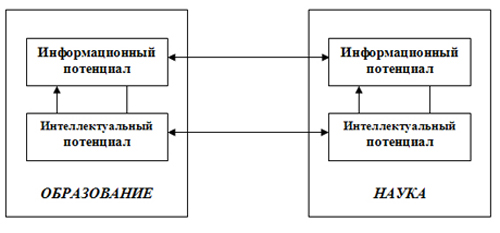
Рис. 1. Структура интеллектуального и информационного дуализма.
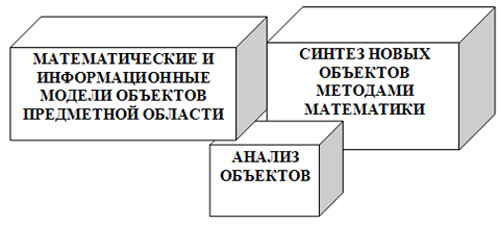
Рис. 2. Триада «модели – анализ – синтез» как вариант концептуального формирования содержания дисциплин.
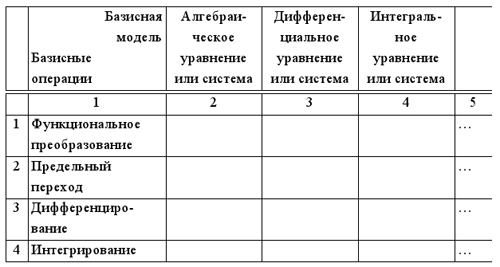
Пример системного структурирования результатов операций над более сложными математическими объектами. Будем использовать базисные операции (действия) и базисные модели, которые определены системной матрицей (табл. 1).
В этой ситуации постоянно изменяется технология творчества личности в виде принципов (рис. 3). Можно определить принципы создания интеллектуальных технологий (рис. 4).
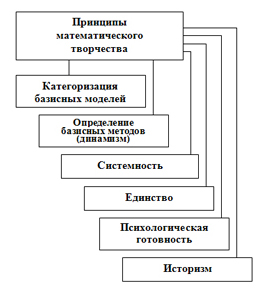
Рис. 3. Иллюстрация принципов математического творчества.

Рис. 4. К формированию системно-интеллектуальных технологий.
Компетентность — интегральная совокупность компетенций, а компетенции — это знания, умения, навыки в определенной профессиональной области и социально-личностные качества, обеспечивающие успешность деятельности выпускников в новых социальных условиях, иллюстрируемые на рис. 5.
Принципы составляют основу подготовки инженерных и научных кадров, которая может трансформироваться с учетом направлений подготовки бакалавров и магистров и специалистов по различным образовательным областям.

Рис. 5. К определению компетентности.
Таким образом, компетентность — комплексная характеристика способности, готовности и необходимости бакалавра, магистра, специалиста применять знания, умения и навыки для создания новых объектов научной деятельности и технологий в различных областях науки, техники.
Интеллектуально-информационный потенциал — это взаимодействующее сочетание интеллектуального и информационного компонентов, способных к взаимному обогащению и непрерывно обобщаемому движению.
Рис. 6. К понятию интеллектуального и информационного потенциалов кадров.
Под высокими интеллектуальными технологиями (ВИТ) будем понимать совокупность организационных мероприятий, методов, системных средств, технологических установок, направленных на формирование новых знаний (за рамками известных технологий, когда уже имеется системная ориентация личности в рамках известных технологий). ВИТ предназначены для естественного формирования основных методов научной деятельности с целью получения нового интеллектуального продукта.
Эти логики как направленные совокупности операций, определяют методы теории знаний.

Рис. 7. Методы теории знаний для формирования содержания образования.
В докладе определены системные варианты применения методов для формирования вариантов содержания образования. Эти варианты даны в табл. 3. Можно определить различные варианты содержания образования для разработки АПИМ (табл. 2).
Формы представления знаний методами теории знаний
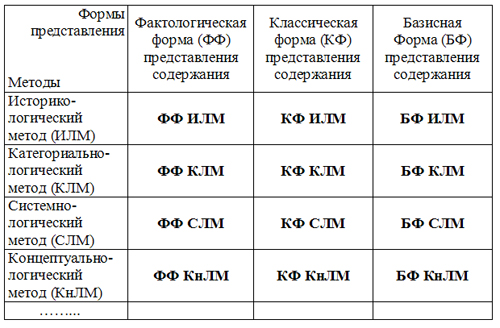
Базисный принцип позволяет формировать компетентностных знаний, умений и навыков (КЗУН) и содержание на основе классов моделей дисциплин, для которых исходными являются комплексы моделей теории знаний для федеральных и других дисциплин.
Историко-логические модели знаний включают дидактические единицы классических программ, строятся на основе экспертных оценок и отражают содержание дисциплин в исторической последовательности создания научных областей знаний (НОЗ). Проекция НОЗ на образовательные дисциплины формируется на основе экспертных оценок разработчиков. Классические модели содержания и знаний используются на первых этапах обучения бакалавров и специалистов, являются исходными для разработки базисных КЗУН. Этот класс программ является наиболее распространенным в российской высшей школе, который реализует естественную модель формирования и передачи знаний. Развитие моделей знаний приводит к следующему классу моделей теории знаний, умений и навыков.
Модели знаний, умений и навыков компетентностного типа формируется на основе структуры научных знаний, а содержание дисциплин формируется как «проекции» концептуальных идей (концепций) из областей научного знания в содержание дисциплин. Эти программы дисциплин формируют знания наиболее общего характера и могут использоваться при обучении в аспирантуре.
Таким образом, предлагаемые классы моделей знаний содержат перечни элементов знаний и определяют три списка: список базисных категорий, список базисных операций и результатов, список базисных методов.
Содержание базисных КЗУН можно дополнить приложениями для высшего и среднего образования. На основе базисных КЗУН можно формировать содержание дисциплин.
Пример. Ниже приводится примеры «укороченных» базисных категориально-логических КЗУН, реализованных в программах по дисциплинам «Математика» и «Электротехника и электроника», необходимые для реализации знаниевой составляющей компетенций.
Математика
1. Линейная алгебра
Базисные категории: матрица; определитель; система линейных алгебраических уравнений (СЛАУ); линейный оператор; собственные числа (СЧ) и собственные векторы (СВ) линейного оператора.
Базисные операции: совокупность операций над базисными категориями.
Базисные методы: методы Крамера, Гаусса, обратной матрицы, Кронекера-Капелли для решения линейных алгебраических систем; методы вычисления СЧ и СВ матриц линейного оператора, решение СЛАУ общего вида.
Приложения. СЛАУ применяются в векторной алгебре, аналитической геометрии, теории неопределенного интеграла, методе наименьших квадратов и других разделах математики.
Остаточные знания.
Применение.
Педагогические измерительные материалы.
2. Производная и дифференциал функции одной переменной.
Базисные понятия: производная, дифференциал, возрастание и убывание функции, локальный экстремум функции.
Базисные операции: совокупность операций над базисными категориями.
Базисные методы: теоремы о производных и дифференциалах; необходимые и достаточные условия экстремума дифференцируемых функций; формула Тейлора для представления функции многочленом; методы вычисления неопределенностей; вычисление приближенных значений функции; правило Лопиталя для вычисления неопределенностей.
Приложения. Дифференцирование применяется в математическом анализе, в естественных науках, экономике, инженерных дисциплинах и др.
Остаточные знания.
Применения.
Педагогические измерительные материалы.
Электротехника
Электрические и магнитные цепи, электрические измерения.
Базисные понятия, явления и элементы: электрический ток, напряжение, потенциал, электродвижущая сила (ЭДС), мощность, энергия, частота, фаза, сопротивление, индуктивность, электрическая емкость, проводимость, резонанс, электрическая цепь, электрическая схема, узел, ветвь, контур; магнитный поток, магнитная индукция, магнитодвижущая сила (МДС) гистерезис, магнитная цепь, магнитопровод.
Базисные операции: совокупность операций над базисными понятиями, явлениями и элементами.
Базисные методы: методы теории функций комплексного переменного на основе различных представления комплексных чисел; методы решения линейных алгебраических систем с комплексными матрицами; методы решения обыкновенных дифференциальных уравнений; методы временных диаграмм; векторный метод; комплексный метод; метод математического моделирования цепей на основе контурных токов; метод эквивалентных преобразований; метод узловых потенциалов; метод эквивалентного генератора.
Остаточные знания.
Применения.
Педагогические измерительные материалы.
Электроника
Базисные понятия, явления и элементы: явление электронно-дырочной проводимости в полупроводниках; основные элементы электронных цепей: диод, тиристор, транзистор, микросхема, выпрямитель, инвертор, пульсации напряжений, фильтры, стабилизатор, импульсный преобразователь, усилитель, обратная связь, операционный усилитель, компаратор, триггер, счетчик импульсов, регистр, дешифратор, мультиплексор, микропроцессор.
Базисные операции: совокупность операций над базисными понятиями, явлениями и элементами.
Базисные методы: методы моделирования статических характеристик электронных цепей с применением непрерывных или разрывных функций; методы математического моделирования процессов транзисторов Эберса-Мола и др.; методы дискретной математики для описания процессов в микросхемах; методы решения дифференциальных уравнений для анализа переходных и установившихся процессов в устройствах аналоговой и цифровой электроники; методы анализа электронных схем с применением ЭВМ.
Остаточные знания.
Применения.
Педагогические измерительные материалы.
Пример. Основные объекты математики определены в табл. 3.
Формирование различных уравнений, неравенств и сравнений
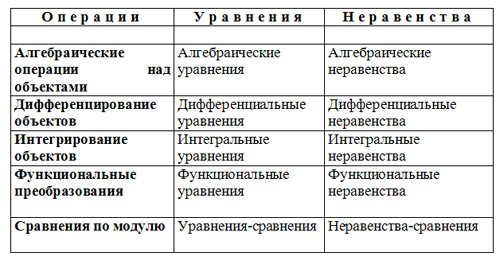
Пример применения в геометрии: поскольку геометрия изучает отношения между геометрическими фигурами, к числу которых относится точки, прямые, фигуры, кривые, плоскости, фигуры, то эти понятия являются категориями, иллюстрируемыми в табл. 4.
К определению базовых категорий геометрий

Применение операций к базисным понятиям позволяет сформировать комплекс заданий по геометрии. Этот пример дает ответ на вопрос о том, какие «операции» можно выполнить над этими категориями для того, чтобы получить контрольные задач.
В этой связи в качестве примера рассмотрим системную характеристику «категорий» и возможных «операций», представленную в табл. 5. К их числу можно отнести действия «сдвиг» и «пересечение». Далее для формирования задачи необходимо дать содержательную формулировку комплекса задач.
Вариант типовой схемы составления задач по геометрии
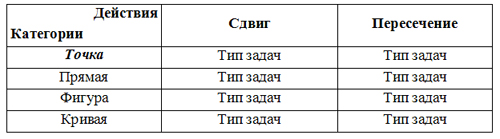
При этом операция «сдвига» порождает новые объекты — категории, а операция «Пересечение» позволяет определить комплекс задач по определению точек попарного пересечения фигур.
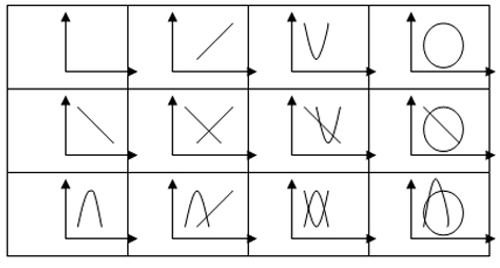
Рис.8. Понятийно-операциональные данные для формирования задач в АПИМ.
Приведенные примеры иллюстрируют применение методов и моделей теории знаний для формирования комплекса подходов к созданию АПИМ для оценки знаний, умений и навыков.
Санкт-Петербургский государственный политехнический университет
ГлавCправ. 2012