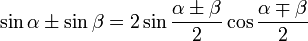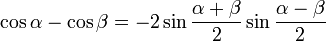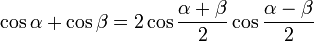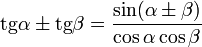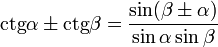Тригонометрические формулы

Основные тригонометрические тождества

• sin² α + cos² α = 1
• tg α · ctg α = 1
• tg α = sin α ÷ cos α
• ctg α = cos α ÷ sin α
• 1 + tg² α = 1 ÷ cos² α
• 1 + ctg² α = 1 ÷ sin² α

Формулы сложения

• sin (α + β) = sin α · cos β + sin β · cos α
• sin (α - β) = sin α · cos β - sin β · cos α
• cos (α + β) = cos α · cos β - sin α · sin β
• cos (α - β) = cos α · cos β + sin α · sin β
• tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
• tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
• ctg (α + β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)
• ctg (α - β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)

Формулы двойного угла

• cos 2α = cos² α - sin² α
• cos 2α = 2cos² α - 1
• cos 2α = 1 - 2sin² α
• sin 2α = 2sin α · cos α
• tg 2α = (2tg α) ÷ (1 - tg² α)
• ctg 2α = (ctg² α - 1) ÷ (2ctg α)

Формулы тройного угла

• sin 3α = 3sin α - 4sin³ α
• cos 3α = 4cos³ α - 3cos α
• tg 3α = (3tg α - tg³ α) ÷ (1 - 3tg² α)
• ctg 3α = (3ctg α - ctg³ α) ÷ (1 - 3ctg² α)

Формулы понижения степени

• sin² α = (1 - cos 2α) ÷ 2
• sin³ α = (3sin α - sin 3α) ÷ 4
• cos² α = (1 + cos 2α) ÷ 2
• cos³ α = (3cos α + cos 3α) ÷ 4
• sin² α · cos² α = (1 - cos 4α) ÷ 8
• sin³ α · cos³ α = (3sin 2α - sin 6α) ÷ 32

Переход от произведения к сумме

• sin α · cos β = ½ (sin (α + β) + sin (α - β))
• sin α · sin β = ½ (cos (α - β) - cos (α + β))
• cos α · cos β = ½ (cos (α - β) + cos (α + β))

Переход от суммы к произведению

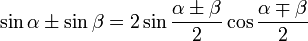
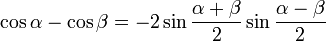
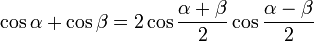
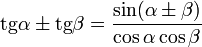
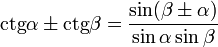
Другие заметки по алгебре и геометрии