Логарифмическая функция

Функция вида   y = log_a х (где а > 0, а ≠ 1)   называется логарифмической.

1) Область определения логарифмической функции — множество всех положительных чисел.
Это следует из определения логарифма, так как выражение log_ax имеет смысл только при x > 0.

2) Множество значений логарифмической функции — множество R всех действительных чисел.
Это следует из того, что для любого действительного числа b есть такое положительное число x, что log_ax = b, т.е. уравнение log_ax = b имеет корень. Такой корень существует и равен
x = a^b, так как log_aa^b = b.

3) Логарифмическая функция y = log_ax является возрастающей на промежутке x > 0, если a > 0, и убывающей, если 0 < a < 1.

4) Если a > 1, то функция y = log_ax принимает положительные значения при x > 1, отрицательные — при 0 < x < 1. Если 0 < a < 1, то функция y = log_ax принимает положительные значения при 0 < x < 1, отрицательные — при x > 1.
Это следует из того, что функция y = log_ax принимает значение , равное нулю, при x = 1 и является возрастающей на промежутке x > 0, если a > 1, и убывающей, если 0 < a < 1.

Ниже представлены графики логарифмических функций при a > 1 (1);   0 < a < 1 (2).

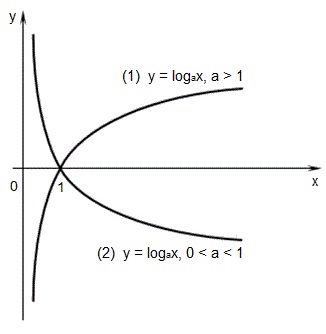
Стоит отметить, что график любой логарифмической функции y = log_ax проходит через точку (1 ; 0)

Другие заметки по алгебре и геометрии