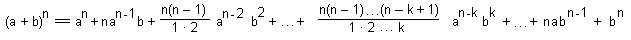Бином Ньютона
Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона:
(a + b)n = an + C1n an - 1 b + C2n an - 2 b2 +...+Ckn an - k bk +... + Cn - 1n abn - 1 + Cnnbn
или (после подстановки выражений Ckn с учетом формулы Ckn = Cn - kn):
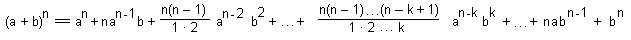 ,
,
где
Ckn —
число всех возможных сочетаний, которые можно образовать
из n элементов по k.
Пример:
(a + b)5 = a5 + C15 a4b + C25 a3b2 + C35 a2b3 + C45 ab4 + C55 b5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
Свойства бинома Ньютона
- Разложение бинома (a + b)n представляет собой многочлен, расположенный по убывающим степеням a (от n-й до нулевой) и по возрастающим степеням b (от нулевой до n-й); сумма показателей a и b в каждом члене разложения равна показателю степени бинома. Число членов разложения на единицу больше показателя степени бинома.
- Коэффициенты членов разложения («биноминальные коэффициенты») возрастают до середины разложения и затем убывают; коэффициенты каждой пары членов, равноотстоящих от начала и конца разложения, равны между собой. Если n четное, то имеется один средний наибольший коэффициент; если n нечетное, то имеется два средних наибольших коэффициента.
- При возведении в n-ю степень разности a - b все четные члены разложения имеют знак "минус":
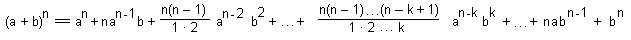
Другие заметки по алгебре и геометрии
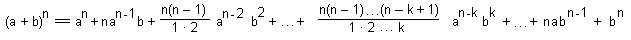 ,
,